Continuous Outcomes: Mean Difference Analysis
mlumr package
2026-02-06
Source:vignettes/continuous_outcomes.Rmd
continuous_outcomes.RmdOverview
This vignette demonstrates how to use ML-UMR for continuous outcomes where the treatment effect is measured as a mean difference (MD). Common applications include: - Change from baseline in HbA1c (diabetes) - Blood pressure reduction (hypertension) - Pain scores (analgesics) - Quality of life measures - Cognitive function scores
Clinical Scenario
Consider comparing two treatments for type 2 diabetes:
- Treatment A (index): New oral antidiabetic agent - IPD available from a Phase 3 trial
- Treatment B (comparator): Standard of care - Only published aggregate data available
The primary endpoint is change from baseline in HbA1c (%) at 24 weeks.
Step 1: Prepare the Data
Simulate Realistic Clinical Trial Data
set.seed(2024)
# --- Index Treatment (IPD) ---
n_index <- 250
# Patient characteristics
ipd_data <- data.frame(
patient_id = 1:n_index,
treatment = "Treatment_A",
# Baseline characteristics (prognostic factors)
age = rnorm(n_index, mean = 58, sd = 10),
baseline_hba1c = rnorm(n_index, mean = 8.5, sd = 1.2),
diabetes_duration = rgamma(n_index, shape = 4, rate = 0.5),
bmi = rnorm(n_index, mean = 31, sd = 5)
)
# True model parameters for Treatment A
alpha_A <- -1.2 # Baseline effect
beta_age <- -0.01 # Older patients respond slightly less
beta_hba1c <- -0.15 # Higher baseline = more reduction
beta_duration <- 0.02 # Longer disease = less response
sigma <- 0.8 # Residual SD
# Generate outcomes
ipd_data$hba1c_change <- with(ipd_data, {
alpha_A +
beta_age * (age - 58) +
beta_hba1c * (baseline_hba1c - 8.5) +
beta_duration * (diabetes_duration - 8) +
rnorm(n_index, 0, sigma)
})
# --- Comparator Treatment (AgD) ---
# Different population (younger, lower baseline HbA1c)
n_comparator <- 200
# True parameters for Treatment B
alpha_B <- -0.8 # Less effective baseline
# Simulate comparator population (not observed)
age_comp <- rnorm(n_comparator, mean = 52, sd = 9)
hba1c_comp <- rnorm(n_comparator, mean = 7.8, sd = 1.0)
duration_comp <- rgamma(n_comparator, shape = 3, rate = 0.5)
y_comp <- alpha_B +
beta_age * (age_comp - 58) +
beta_hba1c * (hba1c_comp - 8.5) +
beta_duration * (duration_comp - 8) +
rnorm(n_comparator, 0, sigma)
# Create aggregate summary (what's published)
agd_data <- data.frame(
study = "Comparator_Study",
treatment = "Treatment_B",
# Outcome summary
mean_change = mean(y_comp),
se_change = sd(y_comp) / sqrt(n_comparator),
# Covariate summaries
age_mean = mean(age_comp),
age_sd = sd(age_comp),
baseline_hba1c_mean = mean(hba1c_comp),
baseline_hba1c_sd = sd(hba1c_comp),
diabetes_duration_mean = mean(duration_comp),
diabetes_duration_sd = sd(duration_comp)
)
# Display summary
cat("IPD Summary (Treatment A):\n")
#> IPD Summary (Treatment A):
cat(" N =", n_index, "\n")
#> N = 250
cat(" Mean HbA1c change =", round(mean(ipd_data$hba1c_change), 2), "%\n")
#> Mean HbA1c change = -1.22 %
cat(" Age (mean/SD):", round(mean(ipd_data$age), 1), "/",
round(sd(ipd_data$age), 1), "\n")
#> Age (mean/SD): 58.4 / 9.9
cat(" Baseline HbA1c (mean/SD):", round(mean(ipd_data$baseline_hba1c), 2), "/",
round(sd(ipd_data$baseline_hba1c), 2), "\n\n")
#> Baseline HbA1c (mean/SD): 8.57 / 1.15
cat("AgD Summary (Treatment B):\n")
#> AgD Summary (Treatment B):
cat(" N =", n_comparator, "\n")
#> N = 200
cat(" Mean HbA1c change =", round(agd_data$mean_change, 2), "%\n")
#> Mean HbA1c change = -0.67 %
cat(" Age (mean/SD):", round(agd_data$age_mean, 1), "/",
round(agd_data$age_sd, 1), "\n")
#> Age (mean/SD): 53.1 / 8.1
cat(" Baseline HbA1c (mean/SD):", round(agd_data$baseline_hba1c_mean, 2), "/",
round(agd_data$baseline_hba1c_sd, 2), "\n")
#> Baseline HbA1c (mean/SD): 7.75 / 0.96Assess Population Imbalance
# The comparator population is younger with lower baseline HbA1c
# This imbalance could bias a naive indirect comparison
cat("\nPopulation Differences:\n")
#>
#> Population Differences:
cat(" Age difference:", round(mean(ipd_data$age) - agd_data$age_mean, 1), "years\n")
#> Age difference: 5.3 years
cat(" Baseline HbA1c difference:",
round(mean(ipd_data$baseline_hba1c) - agd_data$baseline_hba1c_mean, 2), "%\n")
#> Baseline HbA1c difference: 0.82 %Step 2: Set Up ML-UMR Data Structures
Prepare IPD
ipd <- set_ipd_unanchored(
data = ipd_data,
treatment = "treatment",
outcome = "hba1c_change",
covariates = c("age", "baseline_hba1c", "diabetes_duration"),
likelihood = "normal" # Continuous outcome
)
print(ipd)
#> $data
#> # A tibble: 250 × 6
#> .study .trt .outcome age baseline_hba1c diabetes_duration
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 IPD_Study Treatment_A -0.213 67.8 10.6 10.2
#> 2 IPD_Study Treatment_A -1.65 62.7 8.71 4.53
#> 3 IPD_Study Treatment_A -1.85 56.9 9.73 5.31
#> 4 IPD_Study Treatment_A -0.255 55.9 8.17 17.9
#> 5 IPD_Study Treatment_A -0.645 69.6 8.83 12.0
#> 6 IPD_Study Treatment_A -1.67 70.9 6.61 9.47
#> 7 IPD_Study Treatment_A -1.73 63.3 8.68 9.47
#> 8 IPD_Study Treatment_A -2.27 56.7 8.31 4.67
#> 9 IPD_Study Treatment_A -1.14 45.8 9.16 3.94
#> 10 IPD_Study Treatment_A -1.50 46.8 7.12 8.69
#> # ℹ 240 more rows
#>
#> $n
#> [1] 250
#>
#> $n_events
#> [1] NA
#>
#> $treatment
#> [1] "Treatment_A"
#>
#> $covariates
#> [1] "age" "baseline_hba1c" "diabetes_duration"
#>
#> $likelihood
#> [1] "normal"
#>
#> $type
#> [1] "ipd"
#>
#> attr(,"class")
#> [1] "ipd_unanchored" "list"Prepare AgD
agd <- set_agd_unanchored(
data = agd_data,
treatment = "treatment",
outcome_y = "mean_change", # Mean outcome
outcome_se = "se_change", # Standard error
cov_means = c("age_mean", "baseline_hba1c_mean", "diabetes_duration_mean"),
cov_sds = c("age_sd", "baseline_hba1c_sd", "diabetes_duration_sd"),
cov_types = c("continuous", "continuous", "continuous"),
likelihood = "normal"
)
print(agd)
#> $data
#> # A tibble: 1 × 10
#> .study .trt .y .se age_mean age_sd baseline_hba1c_mean
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 AgD_Study Treatment_B -0.665 0.0559 53.1 8.14 7.75
#> # ℹ 3 more variables: baseline_hba1c_sd <dbl>, diabetes_duration_mean <dbl>,
#> # diabetes_duration_sd <dbl>
#>
#> $n
#> [1] NA
#>
#> $n_events
#> [1] NA
#>
#> $treatment
#> [1] "Treatment_B"
#>
#> $covariates
#> [1] "age" "baseline_hba1c" "diabetes_duration"
#>
#> $cov_info
#> $cov_info$age
#> $cov_info$age$mean_col
#> [1] "age_mean"
#>
#> $cov_info$age$sd_col
#> [1] "age_sd"
#>
#> $cov_info$age$type
#> [1] "continuous"
#>
#>
#> $cov_info$baseline_hba1c
#> $cov_info$baseline_hba1c$mean_col
#> [1] "baseline_hba1c_mean"
#>
#> $cov_info$baseline_hba1c$sd_col
#> [1] "baseline_hba1c_sd"
#>
#> $cov_info$baseline_hba1c$type
#> [1] "continuous"
#>
#>
#> $cov_info$diabetes_duration
#> $cov_info$diabetes_duration$mean_col
#> [1] "diabetes_duration_mean"
#>
#> $cov_info$diabetes_duration$sd_col
#> [1] "diabetes_duration_sd"
#>
#> $cov_info$diabetes_duration$type
#> [1] "continuous"
#>
#>
#>
#> $likelihood
#> [1] "normal"
#>
#> $type
#> [1] "agd"
#>
#> attr(,"class")
#> [1] "agd_unanchored" "list"Combine Data
network <- combine_unanchored(ipd, agd)
print(network)
#> Unanchored Comparison Data
#> ===========================
#>
#> Likelihood: normal
#>
#> Index treatment (IPD): Treatment_A
#> - N = 250
#> - Continuous outcome
#>
#> Comparator treatment (AgD): Treatment_B
#> - Continuous outcome (AgD summary)
#>
#> Covariates ( 3 ): age, baseline_hba1c, diabetes_duration
#>
#> Integration points: Not yet added (use add_integration_unanchored())Step 3: Add Integration Points
For continuous covariates, we use normal distributions parameterized by the reported means and SDs:
network <- add_integration_unanchored(
network,
n_int = 100, # More points for 3 covariates
age = distr(qnorm, mean = age_mean, sd = age_sd),
baseline_hba1c = distr(qnorm, mean = baseline_hba1c_mean, sd = baseline_hba1c_sd),
diabetes_duration = distr(qnorm, mean = diabetes_duration_mean, sd = diabetes_duration_sd)
)
#> Computing correlation matrix from IPD...
#> Added 100 integration points for AgD
print(network)
#> Unanchored Comparison Data
#> ===========================
#>
#> Likelihood: normal
#>
#> Index treatment (IPD): Treatment_A
#> - N = 250
#> - Continuous outcome
#>
#> Comparator treatment (AgD): Treatment_B
#> - Continuous outcome (AgD summary)
#>
#> Covariates ( 3 ): age, baseline_hba1c, diabetes_duration
#>
#> Integration points: 100 (QMC with Gaussian copula)Visualize Population Differences
p1 <- plot_covariate_distribution(network, "age") +
labs(title = "Age Distribution")
p2 <- plot_covariate_distribution(network, "baseline_hba1c") +
labs(title = "Baseline HbA1c Distribution")
print(p1)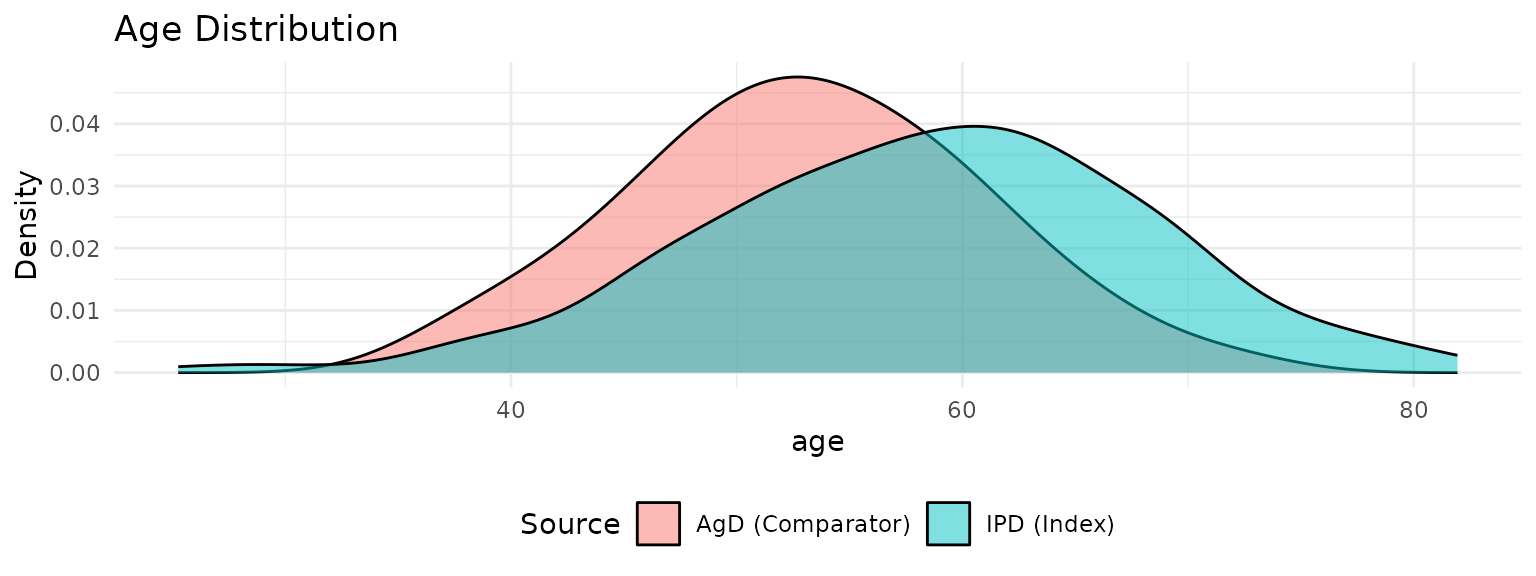
print(p2)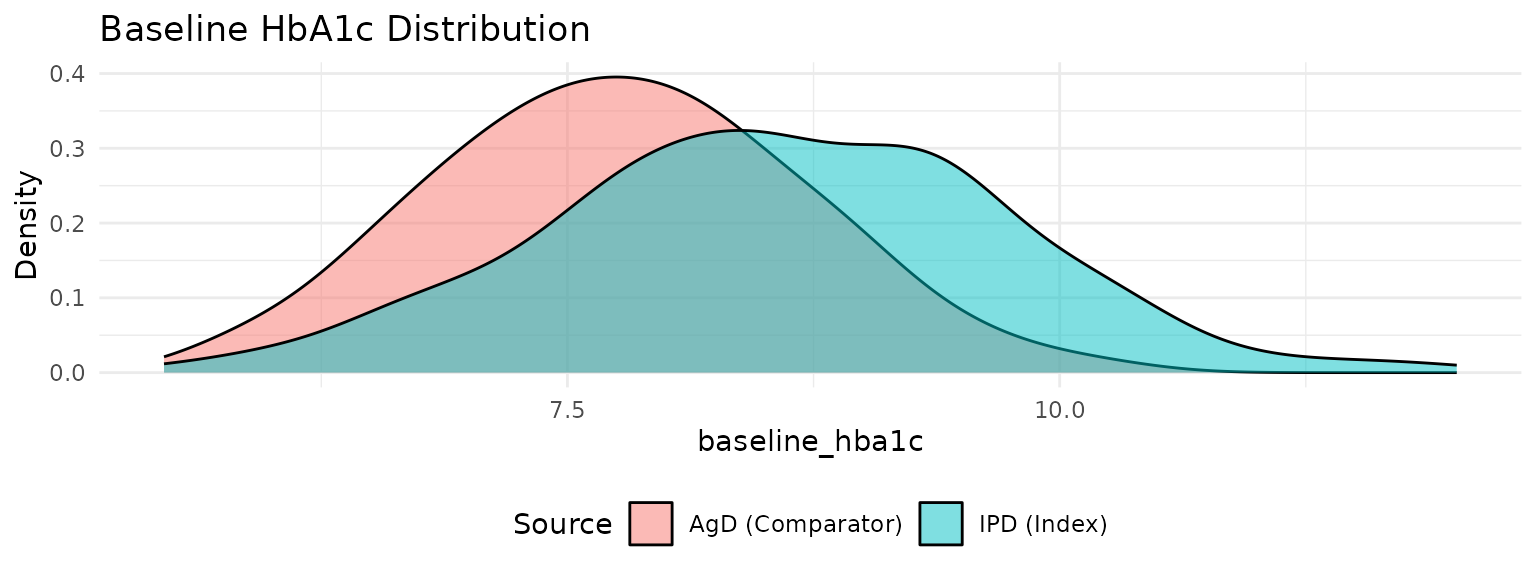
Step 4: Fit ML-UMR Models
Model with SPFA
The SPFA model assumes prognostic factors have the same effect on outcomes regardless of treatment:
fit_spfa <- mlumr(
data = network,
spfa = TRUE,
prior_intercept = prior_normal(0, 5), # Weakly informative
prior_beta = prior_normal(0, 2), # Moderate shrinkage
iter_warmup = 1000,
iter_sampling = 2000,
chains = 4,
seed = 123
)
print(fit_spfa)Model with Relaxed SPFA
The relaxed model allows treatment-specific covariate effects (effect modification):
fit_relaxed <- mlumr(
data = network,
spfa = FALSE,
prior_intercept = prior_normal(0, 5),
prior_beta = prior_normal(0, 2),
iter_warmup = 1000,
iter_sampling = 2000,
chains = 4,
seed = 123
)
print(fit_relaxed)Step 5: Extract and Interpret Results
Mean Difference Estimates
# Extract mean differences in both populations
effects <- marginal_effects(fit_spfa, population = "both", effect_type = "md")
print(effects)Interpretation:
- MD in Index Population: Treatment A vs B effect if both treatments were given to the IPD population (older, higher baseline HbA1c)
- MD in Comparator Population: Treatment A vs B effect if both treatments were given to the AgD population (younger, lower baseline HbA1c)
Forest Plot
plot_marginal_effects_forest(fit_spfa, effect_type = "md") +
labs(x = "Mean Difference in HbA1c Change (%)")Step 6: Model Comparison
# Compare SPFA vs Relaxed models
comparison <- compare_models(fit_spfa, fit_relaxed)Decision criteria:
- If SPFA model has lower DIC: Use SPFA model (simpler, more precise)
- If Relaxed model has lower DIC by >5: Evidence of effect modification; consider using relaxed model or investigating further
Clinical Interpretation
Understanding the Results
Population-Adjusted Effects: Unlike naive comparisons, ML-UMR adjusts for differences in age, baseline HbA1c, and disease duration between populations.
-
Two Target Populations:
- Index population effect: What would happen if comparator patients received Treatment A instead?
- Comparator population effect: What would happen if index patients received Treatment B instead?
Clinical Significance: A mean difference of 0.3-0.5% in HbA1c is typically considered clinically meaningful.
Example Results Interpretation
# Example output (hypothetical values):
#
# Effect Population Mean SD 2.5% 97.5%
# MD Index -0.42 0.15 -0.71 -0.13
# MD Comparator -0.38 0.18 -0.73 -0.04
#
# Interpretation:
# - Treatment A reduces HbA1c by approximately 0.4% more than Treatment B
# - Effect is consistent across populations (similar MD in both)
# - 95% CrI excludes 0, suggesting statistical significance
# - Effect size is clinically meaningful (>0.3%)Special Considerations for Continuous Outcomes
1. Residual Variance
The normal likelihood model estimates a residual standard deviation
(sigma) from the IPD. This captures within-treatment
variability not explained by covariates.
2. Prior Selection
For continuous outcomes, priors should be calibrated to the outcome scale:
# If HbA1c change typically ranges from -3 to +1:
# - Intercept: N(0, 2) covers plausible range
# - Beta: N(0, 1) allows moderate covariate effects
# More informative if you have prior knowledge:
prior_intercept = prior_normal(-1, 1) # Expect negative change
prior_beta = prior_normal(0, 0.5) # Small covariate effects4. Missing Data
Handle missing covariates before analysis:
# Check for missingness
sum(!complete.cases(ipd_data[, c("age", "baseline_hba1c")]))
# Options:
# 1. Complete case analysis (default in set_ipd_unanchored)
# 2. Multiple imputation (pre-process data before mlumr)Summary
This vignette demonstrated:
- Setting up ML-UMR for continuous outcomes with normal likelihood
- Using
outcome_y(mean) andoutcome_se(standard error) for AgD - Interpreting mean difference estimates in different populations
- Accounting for population differences in prognostic factors
For binary outcomes, see the main tutorial vignette. For count/rate outcomes, see the “Count and Rate Outcomes” vignette.
Session Information
sessionInfo()
#> R version 4.5.2 (2025-10-31)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 24.04.3 LTS
#>
#> Matrix products: default
#> BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so; LAPACK version 3.12.0
#>
#> locale:
#> [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
#> [4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
#> [7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
#> [10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
#>
#> time zone: UTC
#> tzcode source: system (glibc)
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] ggplot2_4.0.2 dplyr_1.2.0 mlumr_0.1.0
#>
#> loaded via a namespace (and not attached):
#> [1] sass_0.4.10 utf8_1.2.6 generics_0.1.4
#> [4] lattice_0.22-7 digest_0.6.39 magrittr_2.0.4
#> [7] evaluate_1.0.5 grid_4.5.2 RColorBrewer_1.1-3
#> [10] mvtnorm_1.3-3 fastmap_1.2.0 jsonlite_2.0.0
#> [13] Matrix_1.7-4 rngWELL_0.10-10 purrr_1.2.1
#> [16] scales_1.4.0 stabledist_0.7-2 randtoolbox_2.0.5
#> [19] numDeriv_2016.8-1.1 textshaping_1.0.4 jquerylib_0.1.4
#> [22] cli_3.6.5 rlang_1.1.7 pspline_1.0-21
#> [25] gsl_2.1-9 withr_3.0.2 cachem_1.1.0
#> [28] yaml_2.3.12 tools_4.5.2 copula_1.1-6
#> [31] vctrs_0.7.1 R6_2.6.1 stats4_4.5.2
#> [34] lifecycle_1.0.5 ADGofTest_0.3 fs_1.6.6
#> [37] ragg_1.5.0 pcaPP_2.0-5 pkgconfig_2.0.3
#> [40] desc_1.4.3 pkgdown_2.2.0 pillar_1.11.1
#> [43] bslib_0.10.0 gtable_0.3.6 glue_1.8.0
#> [46] systemfonts_1.3.1 xfun_0.56 tibble_3.3.1
#> [49] tidyselect_1.2.1 knitr_1.51 farver_2.1.2
#> [52] htmltools_0.5.9 labeling_0.4.3 rmarkdown_2.30
#> [55] compiler_4.5.2 S7_0.2.1